A* for 2D path finding
I wrote this almost a year ago, but never posted it since I didn’t get a chance to fully comment the code. Since I probably won’t get around to it any time soon, I’m posting it now. I even shoddily converted it into a java applet!
Here’s a simple 2D shortest path planning algorithm written in Java.
First, here’s the Applet. Draw the walls of the maze by dragging the mouse while holding down the left mouse button. Then right click somewhere to set the start point, and somewhere else to set the end point. Right click again to reset the applet.
This takes the form a a java applet that used to be included here, but those are pretty much unviewable these days.
I’ve spent a bit of time brushing up on some algorithms and data structure basics. As a for-fun project (and to make sure I still remember how to code in Java) I decided to see how quick I could make graphical java program to play around with the A* search algorithm. It seemed like it would be a simple solution to a problem that I had run into several times in the past.
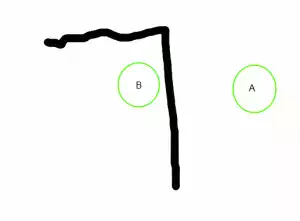
When I was first learning to code I made some simple top down 2D games. I would often have had to solve the problem of finding the shortest path from point A to point B while navigating obstacles as shown crudely below:
I think I remember copy/pasting some black box code I found on the internet and never giving the problem much thought.
Later in college, the final project for a computer science course was to piece together a Pacman game. Part of the project involved implementing the AI for the ghosts by using Dijkstra’s algorithm , It wasn’t a particularly efficient solution, but was part of the project’s requirements.
In my algorithm review I came across the A* search algorithm. I had seen it previously used in path planning for robotic applications, but I hadn’t realized that one way to think about it is as Dijkstra’s algorithm with the edition of a heuristic to improve the search order. I decided to try my hand at adapting it to solve the 2D shortest path problem.
I based my code on the A* Wikipedia page. Here it is for posterity:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
function A*(start,goal)
closedset := the empty set // The set of nodes already evaluated.
openset := {start} // The set of tentative nodes to be evaluated, initially containing the start node
came_from := the empty map // The map of navigated nodes.
g_score[start] := 0 // Cost from start along best known path.
// Estimated total cost from start to goal through y.
f_score[start] := g_score[start] + heuristic_cost_estimate(start, goal)
while openset is not empty
current := the node in openset having the lowest f_score[] value
if current = goal
return reconstruct_path(came_from, goal)
remove current from openset
add current to closedset
for each neighbor in neighbor_nodes(current)
if neighbor in closedset
continue
tentative_g_score := g_score[current] + dist_between(current,neighbor)
if neighbor not in openset or tentative_g_score < g_score[neighbor]
came_from[neighbor] := current
g_score[neighbor] := tentative_g_score
f_score[neighbor] := g_score[neighbor] + heuristic_cost_estimate(neighbor, goal)
if neighbor not in openset
add neighbor to openset
return failure
function reconstruct_path(came_from, current_node)
if came_from[current_node] is set
p := reconstruct_path(came_from, came_from[current_node])
return (p + current_node)
else
return current_node
For me the easiest way to think about this algorithm relates back to the rule that the heuristic_cost_estimate must obey. The goal of A* is to find the minimum cost path between two nodes. It uses the true cost that it’s calculated so far, along with a heuristic estimate of the cost to unexplored nodes to try to pick the best node to search next. In order for the search to find the true shortest past the heuristic must be admissible. A heuristic is admissible if it never overestimates the cost.
To put this into terms of the 2D path problem, the cost is going to be shortest distance from a given point to the target point. For my simple demo I’m going to make the world out of tiles that can be traversed by going up, down, left or right. Some tiles will be treated as impassible walls. In the absence of any walls the distance from point A to B is abs(A.x-B.x) + abs(A.y-B.y) . This provides a perfect heuristic for the A* search, since the presence of walls can only increase the minimum path.
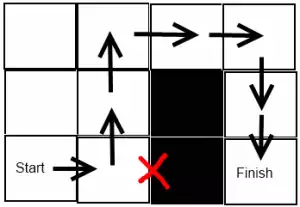
The heuristic predicted cost for this example is 3. Due to the obstacle the actual cost is 7.
For each step of the A* search, the most likely node (in this case tile) that is predicted to bring us closest to our goal is evaluated. The neighboring tiles have their costs predicted and our added to our pool of potential tiles for our next iteration. The key to the admissibility rule is that if our predictions ever overestimated the cost of a tile, this might cause the tile to never be evaluated and the true shortest path might be skipped.
Now for my implementation. Note that this was done as quickly and simply as possible, and is not the worlds cleanest or most efficient code.
First, this is how I decided to represent the map of the game world.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
//2D matrix of map tiles. The index of each tile is its x-y coordinate on the map.
final TileItem mapGrid[][];
//The screen size in pixels
final static int DEFAULT_WIDTH = 800;
final static int DEFAULT_HEIGHT = 400;
//The size of the map in tiles. Each tile will be DEFAULT_WIDTH/DEFAULT_MAP_WIDTH by DEFAULT_HEIGHT/DEFAULT_MAP_HEIGHT pixels
final static int DEFAULT_MAP_WIDTH = 80;
final static int DEFAULT_MAP_HEIGHT = 40;
//enum to store how a cell should be drawn, and whether it can be passed through
enum CellType {
//this tile will be the start point of the search
START,
//this tile will be the stop point of the search
STOP,
//this tile will be transversable
OPEN,
//this tile was found on the shortest path
PATH,
//this tile was searched, but not on the shortest path
SEARCHED,
//this tile is not transversable
CLOSED
}
//Represents a tile on the map
class TileItem implements Comparable {
//x-y coordinate location of tile
public Point point;
//guess at best distance from start to finish of a path that goes
//through this point
public Double fScore;
//best distance from start to this tile found so far
public Double gScore;
//how a tile should be drawn, and whether it can be passed through
public CellType type;
//This method is used by the priority queue to determine the presidence of entries
//normailally the astar only evaluates the fscore, but this can make the search time
//longer then necesary when there are many equal length paths. This function effectively
//will cause the priority queue to sort by shortest path through the tile, and then break ties
//By valuing paths that are the farthest away from the starting point.
@Override
public int compareTo(TileItem arg0) {
if(!arg0.fScore.equals(fScore)) {
return fScore.compareTo(arg0.fScore);
}
return arg0.gScore.compareTo(gScore);
}
}
Next, here is the my implementation of the search algorithm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
void Search() {
PriorityQueue<TileItem> test=new PriorityQueue<>();
test.add(new TileItem());
ArrayList<Point> closedSet = new ArrayList<>();
HashMap<Point, Point> cameFrom = new HashMap<>();
PriorityQueue<TileItem> openSet=new PriorityQueue<>();
TileItem goal = null;
TileItem start = null;
for (int r = 0; r < DEFAULT_MAP_HEIGHT; r++) {
for (int c = 0; c < DEFAULT_MAP_WIDTH; c++) {
if (mapGrid[r][c].type == CellType.START) {
start = mapGrid[r][c];
} else if (mapGrid[r][c].type == CellType.STOP) {
goal = mapGrid[r][c];
}
}
}
start.gScore=0.0;
start.fScore=0.0 + huiristic(start.point,goal.point);
openSet.add(start);
while (!openSet.isEmpty()) {
TileItem current = openSet.poll();
if (current.equals(goal)) {
for (Point step : closedSet) {
mapGrid[step.y][step.x].type = CellType.SEARCHED;
}
Point backTrack = goal.point;
while (!backTrack.equals(start.point)) {
backTrack = cameFrom.get(backTrack);
mapGrid[backTrack.y][backTrack.x].type = CellType.PATH;
}
return;
}
// System.out.println("Cur "+current.point + " "+current.fScore+ " "+current.gScore);
openSet.remove(current);
closedSet.add(current.point);
double tentativeGScore=current.gScore+1;
TileItem[] consider = new TileItem[4];
consider[0]=(current.point.x > 0)?mapGrid[current.point.y][current.point.x - 1]:null;
consider[1]=(current.point.x < DEFAULT_MAP_WIDTH-1)?mapGrid[current.point.y][current.point.x + 1]:null;
consider[2]=(current.point.y > 0)?mapGrid[current.point.y-1][current.point.x]:null;
consider[3]=(current.point.y < DEFAULT_MAP_HEIGHT-1)?mapGrid[current.point.y+1][current.point.x]:null;
for (int i=0; i<4 ; i++) {
if(consider[i]==null
||closedSet.contains(consider[i].point)
|| consider[i].type == CellType.CLOSED ){
continue;
}
if (!openSet.contains(consider[i]) || tentativeGScore < consider[i].gScore) {
if (openSet.contains(consider[i])) {
//should never happen!
openSet.remove(consider[i]);
System.out.println("WTF!");
}
consider[i].fScore=tentativeGScore + huiristic(consider[i].point,goal.point);
cameFrom.put(consider[i].point, current.point);
consider[i].gScore=tentativeGScore;
// System.out.println("Con "+i+" " +consider[i].point + " "+consider[i].fScore+ " "+consider[i].gScore);
openSet.add(consider[i]);
}
}
}
for (Point step : closedSet) {
mapGrid[step.y][step.x].type = CellType.SEARCHED;
}
}
Lastly, this is the huiristic I decided to use along with some commented out alternatives.
1
2
3
4
5
6
7
8
9
double huiristic(Point eval,Point goal)
{
//not admisable
//return eval.distanceSq(goal);
//return eval.distance(goal);
return Math.abs(eval.x-goal.x)+Math.abs(eval.y-goal.y);
//return 0;
}
The A* search will perform an identical search to Dijkstra’s algorithm if the heuristic prediction is always 0. This case is clearly admissible, but completely ignores the fact that going in the general direction of the target is desirable.